Cálculo - Integral
|
1.2 ÁREA BAJO LA CURVA
Actividad 1: En tu cuaderno: Recuerda y Representa una grafica del comportamiento del velocímetro: Si manejas tu auto “Expedition” a una velocidad constante de 80 km/hr durante 3 horas. Identifica: 1. ¿Qué información representa el eje “x”? 2. ¿Qué información representa el eje “y”?
Actividad 2: Ilumina el área bajo la gráfica correspondiente a las tres horas. Calcula el área, ¿Qué información obtienes al calcular el área iluminada? - R= el cálculo de la distancia
Actividad 3: Participa en una tómbola y en equipos de 3 estudiantes: Determina la representación gráfica y la distancia recorrida, si viajaste durante: 1. 5 hora; ¿Qué distancia recorriste de la segunda a la tercera hora? Ilumina el intervalo de tiempo. 2. 4 horas; ¿Qué distancia recorriste de la primera a la tercera hora? Ilumina el intervalo de tiempo. 3. 6 horas; ¿Qué distancia recorriste de la primera a la quinta hora? 4. 7 horas; ¿Qué distancia recorriste de la tercera a la sexta hora? 5. x horas. ¿Qué distancia recorrió del tiempo “a” al tiempo “b”?, Ilumina cada intervalo de tiempo.
Establece una expresión algebraica que te ayude a: ¿Cómo calcular el área bajo la curva para x horas con 80km/hr?
Reflexiona, Analiza y establece la función d(t), que relacione la distancia recorrida “d” y el tiempo transcurrido t. (Ya lo tienes)
Redacta la relación entre la función que obtuviste con el comportamiento del velocímetro de tu auto:
OJO: Ahora que sabes que la gráfica es la derivada (“v(t) = 80”) de la función distancia “d(t)” en el intervalo [0, 3], podemos concluir que el resultado es la sustitución en: d(3)= 80*3. |
|||||
|
Leer la página 53 - 56. (Da clic sobre el libro.) |
|||||
|
Actividad 2: Escribe en tu cuaderno la explicación del autor de cómo calcular el área bajo la curva y los ejemplos 1 y 2. |
|||||
|
Integral de Riemann. volviendo a una función cualquiera y recordando que |
|||||
|
|
|||||
|
De aquí se puede deducir que si se halla el límite cuando el número de rectángulos sea muy grande o cuando las longitudes de las bases de esos rectángulos sean muy pequeñas, se logrará la mejor y más exacta aproximación del área. Esto se representa así: |
|||||
|
|
|||||
|
Con esto ya se encontró la mejor aproximación del área. Ahora sí se puede enunciar la integral definida ya que:
|
|||||
|
Ejemplo (revisa las reglas de derivadas- página 59)
|
|||||



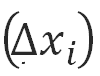 representa cada una de las particiones de la región, si ésta se hace tan pequeña como se pueda, se obtendrán un mayor número de rectángulos que dará una mejor aproximación al área que se busca, como se puede observar en la siguiente figura:
representa cada una de las particiones de la región, si ésta se hace tan pequeña como se pueda, se obtendrán un mayor número de rectángulos que dará una mejor aproximación al área que se busca, como se puede observar en la siguiente figura: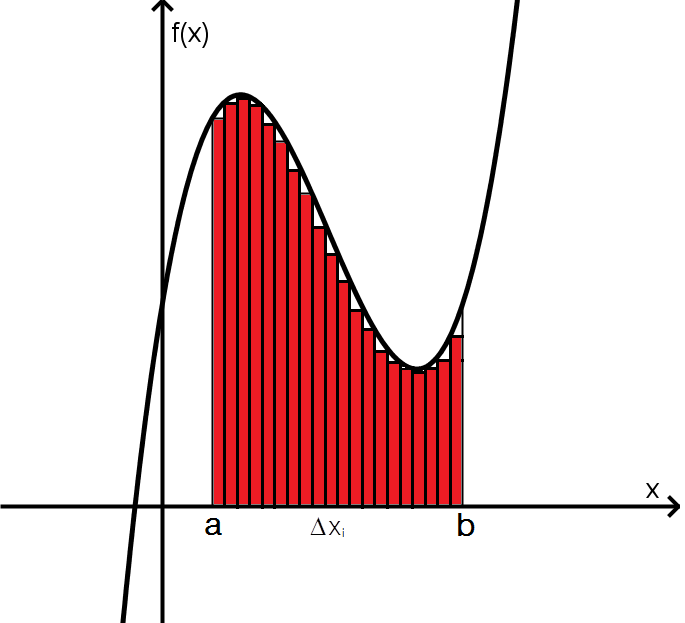
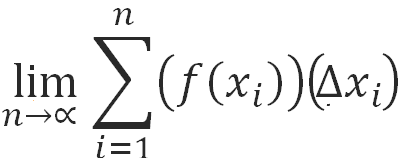
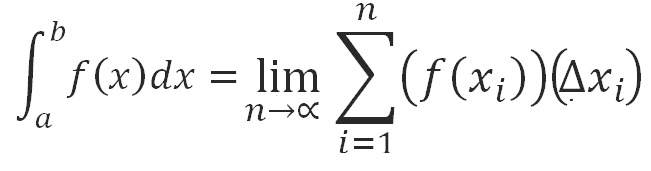
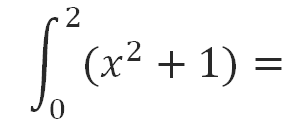
Tema: Integral
Asunto: :p
Si profa :v
Responder
Asunto: Hola
good
Responder
Asunto: Re: Hola
Hola Luis esperando que este sea un medio agradable de comunicación.
Responder